2020年6月1日
<サブスク会計学>サブスクリプションとは何だろう
期間想定がないときのLTVと現在価値の計算

<要旨>
LTVは平均単価に平均継続期間を乗じることで算出できますが、期間の想定が無いなど平均継続期間を把握することが困難なことも多々あります。そのようなときは解約率を用いることで平均継続期間を推計することが可能です。さらに、解約率によって計算したLTVであっても現在価値を計算することが可能です。そもそも正しい解約率とは何かという別の問題が想起されるものの、期間把握の難しさを考えれば解約率によってLTVが計算できることの利便性は無視できません。
1.はじめに
サブスクリプションは「顧客との継続的な関係が担保された状態」のビジネスです。当然、想定する期間は継続的なものになります。ですが、LTVにしても、前回のNPVにしても、この連載では収益を得られる期間が有限であることを暗黙のうちに前提に置いて説明していました。
例えば、一部の乳幼児向けサービスのようにユーザーが一定の年齢に達すると終了したり、提供期間が限定されていて、ある期日が到来すると契約が更新されなかったりと利用が継続されないことが確実な場合はそれでよいかもしれません。しかし、現実には期間があってないような場合が多くあります。そうなると期間の継続をどう考えるか、どうやってLTVを計算するのかに工夫が必要になります。
2.期間算定の難しさ
携帯電話のように、解約を申し出ない限り自動更新で契約が継続されるサービスは珍しくありません。ユーザーが消費者であれば、それこそ一生涯が利用継続期間になるかもしれません。ですが、サービスの利用ユーザーが企業等の法人の場合は人間と違って寿命がありませんので、永遠に契約を自動更新することも可能です。逆に、最低利用期間の定めがなく、いつでも契約できて、いつでも解約できるといった期間があってないようなものもあります(※1)。
休止期間の算入可否の問題もあります。もともと契約していたものをいったん解約して、一定期間をおいて改めて契約した場合、もしくは、解約はしていないものの、利用を中止し課金を一定期間停止してから再開した場合などが休止期間に該当します。休止期間が短期であれば計算結果への影響は僅かなものになるかもしれませんが長期になると無視できなくなってきます。
顧客のサービス利用開始時期によって利用継続期間が著しく異なる場合も期間算定が難しくなります。例えば、サービス開始の草創期は品質が低くて利用者の平均継続期間が短く、後に品質改善により平均継続期間が延びた。このような場合、期間算定のためのデータに草創期の顧客を入れてしまうと平均値が品質改善後の実態よりも下がってしまいますので、そもそも期間算定するためのデータをどのように抽出すべきかという課題が生じてしまいます(※2)。
3.有限の期間によるLTVの過小評価
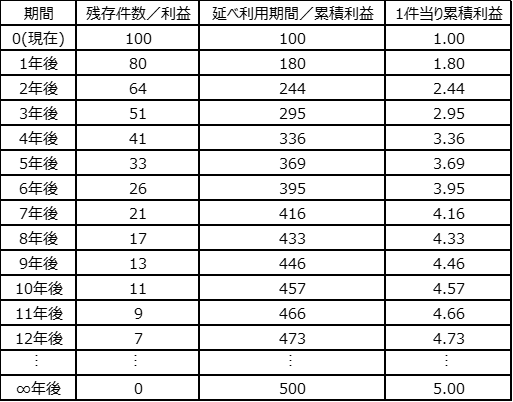
有期でないサブスクリプションのLTVを有限の期間を用いて計算すると過小評価することになるので、投資意思決定や健全性判断にも影響があります。図1をみてください。例えば、ある時点に獲得した契約件数が100件で1件当たりの1年間の利益が1万円だとすると、1年目の利益は100万円となります。獲得した100件は顧客からの申し出がない限り1年間の自動更新とし、毎年一定の割合で解約が発生するとした場合、仮に解約率が20%だとすると2年目の残存件数は80件で利益80万円、以下、3年目は64件で64万円、4年目は51件で51万円、5年目は41件で41万円と年々減少していくことになります。ここで仮に3年などと任意の期間を設定して獲得した契約100件のLTVを244万円もしくは平均して契約1件当たり2.44万円とすれば、4年目以降の利益をLTVに含まないことになります。そもそも3年でそのサブスクリプションの提供を止める想定だったのであれば話は別ですが、このように期限を短く区切るとLTVを過小評価してしまいユニットエコノミクスが小さくなるため本来投資すべきものに投資しなかったり、健全性の判断を間違って撤退すべきでないのに撤退するといったことも起こらないとは限りません。
4.期間想定の無い場合の期間算定
例えば、今日、顧客Aと顧客Bからそれぞれ1件ずつの合計2件の期間想定の無い契約を獲得したとして、この2件の契約の平均継続期間を知ろうとすると、顧客Aが2年で解約し、顧客Bが3年で解約したとすれば、延べの利用継続期間が5年で契約が2件なので平均継続期間が2.5年だということが事後的に分かります。もし、顧客Bが解約せずに継続中であれば平均継続期間は延びていきます。顧客Bとの契約がこのまま継続されれば、平均継続期間は顧客Bに解約されるまで算出できないことになります。
そこで、期間想定の無い場合は解約率によって期間を推計する方法が用いられます。図1の例では解約率が20%と想定しました。毎年20%ずつ契約が減っていけば最終的に契約が0件になります。その時の延べの利用継続期間は500年となりますので(※3)、契約件数100件で除すると平均期間は5年と推計されます(※4,5)。このように解約率さえ分かっていれば実際の延べ利用継続期間が未知であっても平均継続期間が推計できるのです(※6)。LTV、平均継続期間、解約率の関係をまとめると図2になります。

5.期間想定の無い場合の現在価値LTV
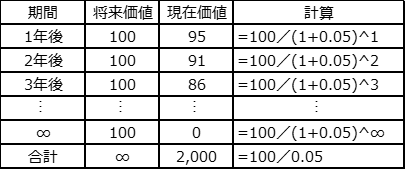
期間が未知であっても解約率が既知であれば平均継続期間が推計されるのでLTVが計算可能となりました。しかし、ここで終わってはいけません。投資採算を計算するにはLTVを現在価値に割り引く必要があります。 解約率を用いてLTVを計算した場合、契約が0件になるまでの年数(つまり無限年)の将来までの利益を現在価値に戻す必要があります。まず解約率を見込まず毎年同じ額の利益が得られる場合を考えます。例えば毎年100万円の利益が得られるとして、割引率が5%であれば図3のようになります。この時の現在価値LTV2,000万円は100万円を割引率の5%で除することで求められます。(※7)無限の年数を現在価値に割り引く計算式はこのように非常にシンプルです。(※8)
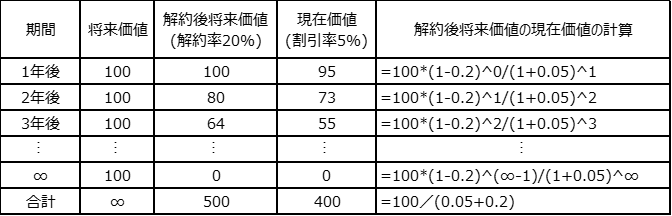
図3の条件に解約率を追加したものが図4です。図1の例のように解約率が20%で一定であれば毎年の100万円が20%ずつ減っていくことになります。このときの現在価値LTV400万円は割引率5%と解約による減少率20%の合計である25%で100万円を除することで求められます(※9)。無限年を想定したLTVの現在価値を求める計算式は図5のとおりです。補足ですが、逆に、一定割合で毎年の利益が増える場合は割引率から増加率を控除することで現在価値が求められます。

6.おわりに
LTVを計算するにあたり、平均継続期間を把握できないことがあります。そのときは解約率を使うことでLTVが計算可能です。また、解約率を使ったLTVであっても現在価値に割り引くことが可能です。解約率をどのように計測するかという別の問題はあるものの期間を把握できなくてもLTVの計算が可能であることの実務上の利便性は無視できないでしょう。
(※1) 売り切り型でリピーターが継続的に利用している状況もこれに含めていいかもしれません。
(※2) データ抽出は期間算定だけではなく解約率の決定においても課題となりますがここではいったん脇に置いておきます。
(※3) 延べ継続期間500年=契約100件/解約率20% 無限等比級数の和の公式より、a+ar^1+ar^2‥‥=a/(1-r) 今回の例はa:100、r:1-20%なので、100/1-(1-0.2)=100/0.2=500 つまり契約数を解約率で除すると延べ継続期間が算出されますので図2の⑤が成り立ちます。
(※4) 平均継続期間5年=延べ継続期間500年÷契約100件
(※5) 図1は年間での解約率をもとに年単位の期間を推計しましたが、月次解約率を使えば月単位の推計となります。
(※6) 数学的な証明は「ユーザの平均継続期間が「1/解約率」で求められることの数学的証明」が分かりやすいです。
(※7)毎年の利益100/割引率0.05=LTV2000万円。無限等比級数の公式よりa+ar^1+ar^2‥‥=1/1-rのaを右辺に移行すると
ar^1+ar^2‥‥=1/(1-r)-a=(a-a(1-r))/1-r=ar/1-r=a/(1/r-1)
ここはa:100 r:1/(1+0.05)⇒1/r:1+0.05なので100/(1.05-1)=100/0.05=2000
(※8) 永久債の説明としてファイナンスの世界で広く知られています。石野(2011)を参照ください
(※9) (a(1+g)^0+a(1+g)^1+a(1+g)^2‥‥)/(a/(1+r)^1+a/(1+r)^2+‥‥)=a/(r-g) ここはa:100 g:-0.2 r:0.05なので100/0.05-(-0.2)=100/0.25=400 考え方は「ファイナンス基礎理論 第7回「現在価値とは」」が参考になります。
参考文献
・石野雄一, 2011.6.20, 『道具としてのファイナンス』, 日本実業出版社
・「ユーザの平均継続期間が「1/解約率」で求められることの数学的証明」, 2017.3.8
https://migi.hatenablog.com/entry/churn-formula
・「ファイナンス基礎理論 第7回「現在価値とは」」, 2007.1.16
http://www.yuichiro-itakura.com/essay/partner_essay/by/by_7.html
